поверхневі хвилі

Наступний цікавий тип хвиль, які, безсумнівно, бачив кожен і які зазвичай в елементарних курсах служать прикладом хвиль, - це хвилі на поверхні води. Ви скоро переконаєтеся, що більш невдалий приклад придумати важко, бо вони анітрохи не схожі ні на звук, ні на світло; тут зібралися всі труднощі, які тільки можуть бути в хвилях. Давайте почнемо з довгих хвиль на глибокій воді. Якщо вважати океан нескінченно глибоким і на його поверхні відбуваються якісь збурення, то виникнуть "хвилі. Взагалі кажучи, можливі будь-які обурення, але синусоидальное рух з дуже невеликим обуренням дає хвилі, що нагадують звичайні гладкі океанські хвилі, що йдуть до берега. Вода, зрозуміло , в середньому залишається на місці, а рухаються самі хвилі. Що ж це за рух - поперечне або поздовжнє? воно не може бути ні тим, ні іншим: ні поперечним, ні поздовжнім. Хоча в кожному даному місці горби чергуються з западинами, воно не може побут рухом вгору і вниз просто через закон збереження кількості води. Куди повинна подітися вода з западини? Адже вона ж практично нестислива. Швидкість хвиль стиснення, т. е. звуку в воді, у багато разів більше: ми зараз їх не розглядаємо. Отже , для нас зараз вода нестислива, тому при утворенні западини вода з цього місця може рухатися тільки в сторони. Так воно і виходить насправді: частинки води поблизу поверхні будуть рухатися приблизно по колу. Як-небудь, коли ви будете ніжитися на воді, лежачи на колі, і прийде такий гладкий вал, подивіться на сусідні предмети і ви побачите, що вони рухаються по колах. Так що картина виходить несподівана: тут ми маємо справу з сумішшю поздовжніх і поперечних хвиль. Зі збільшенням глибини кола зменшуються, поки на достатній глибині від них нічого не залишиться (фіг. 51.9).

Дуже цікаво визначити швидкість таких хвиль. Це повинно бути якийсь комбінацією щільності води, прискорення сили тяжіння, яка в даному випадку є відновлювальної силою, і, можливо, довжини хвилі і глибини. Якщо ми розглянемо випадок нескінченної глибини, то швидкість більше не буде залежати від неї. Але яку б формулу для фазової швидкості хвиль ми не взяли, вона повинна містити ці величини в такій комбінації, щоб давати правильну розмірність. Випробувавши безліч різних способів, ми знайдемо, що тільки одна комбінація g і λ може дати нам розмірність швидкості, саме √ (gλ), яка зовсім не включає щільності. Насправді ця формула для фазової швидкості не цілком точна, і повний аналіз динаміки, в який ми не будемо входити, показує, що все дійсно вийде так, як у нас, за винятком √ (2 π), т. Е.

Цікаво, що довгі хвилі біжать швидше коротких. Так що коли проходить далеко моторний човен створює хвилі, то після певного проміжку часу вони досягнуть берега, але спочатку це будуть рідкісні сплески, оскільки першими приходять довгі хвилі. Потім приходять хвилі стають все коротшими і коротшими, бо швидкість падає як квадратний корінь з довжини хвилі.

«Це ж не так, - може заперечити хтось, - адже щоб робити таке твердження, ми повинні дивитися на групову швидкість». Правильно, звичайно. Формула для фазової швидкості не говорить нам про те, що приходить першим; про це може нам сказати тільки групова швидкість. Так що ми повинні отримати групову швидкість і ми зможемо показати, що вона дорівнює половині фазовоїшвидкості. Для цього потрібно лише згадати, що фазова швидкість поводиться як квадратний корінь з довжини хвилі. Так само, т. Е. Як квадратний корінь з довжини хвилі, поводиться і групова швидкість. Але як може групова швидкість бути вдвічі менше фазової? Подивіться на групу хвиль, викликаних проходить повз човном, і простежте за якимось певним гребенем. Ви виявите, що він біжить разом з групою, але поступово стає все менше і менше, а дійшовши до переднього фронту, зовсім вмирає. Але таємничим і незбагненним чином на зміну йому з заднього фронту піднімається слабенька хвиля і стає вона все сильніше і сильніше. Коротше кажучи, по групі рухаються хвилі, тоді як сама група рухається вдвічі повільніше цих хвиль.

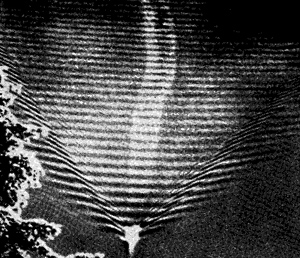Оскільки групова і фазова швидкості не рівні один одному, то хвилі, викликані рухом об'єкта, будуть вже не просто конічними, а набагато більш складними і цікавими. Ви можете бачити це на фіг. 51.10, де показані хвилі, викликані рухається по воді човном. Зауважте, що вони зовсім не схожі на те, що ми отримували для звуку (коли швидкість не залежить від довжини хвилі), де фронт хвилі був просто розповсюджується в сторони конусом. Замість нього ми отримали хвилі позаду рухомого об'єкту, фронт яких перпендикулярний його руху, та ще рухаються під іншими кутами невеликі хвилі з боків. Всю цю картину руху хвиль в цілому можна дуже красиво відтворити, знаючи тільки, що фазова швидкість пропорційна квадратному кореню з довжини хвилі. Весь фокус полягає в тому, що картина хвиль стаціонарне щодо човни (рухається з постійною швидкістю); всі інші види хвиль відстануть від неї.

До сих пір ми розглядали довгі хвилі, для яких відновлювальної силою була гравітація. Але коли хвилі стають дуже короткими, то основний відновлювальної силою виявляється капілярний тяжіння, т. Е. Енергія поверхневого натягу. Для хвиль поверхневого натягу фазова швидкість дорівнює

де Т - поверхневий натяг, а ρ - щільність. Тут все навпаки: чим коротше довжина хвиль, тим більшою є фазова швидкість. Якщо ж діють і сила тяжіння і капілярна сила, як це зазвичай буває, то ми отримуємо комбінацію

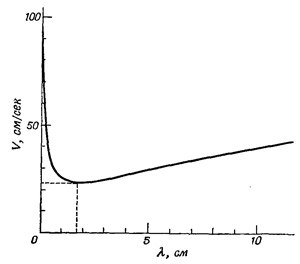де k = 2 π / λ - хвильове число. Як бачите, швидкість хвиль на воді - річ дійсно досить складна. На фіг. 51.11 показана фазова швидкість як функція довжини хвилі. Вона велика для дуже коротких хвиль, велика для дуже довгих хвиль, але між ними існує деяка мінімальна швидкість поширення. Виходячи з цієї формули, можна обчислити і групову швидкість: вона виявляється рівною 3/2 фазової швидкості, так для ряби і 1/2 фазовоїшвидкості для хвиль «тяжкості». Зліва від мінімуму групова швидкість більше фазової, а праворуч групова швидкість менше. З цим фактом пов'язано кілька цікавих явищ. Оскільки групова швидкість зі зменшенням довжини хвилі швидко збільшується, то, якщо ми створимо якісь збурення, виникнуть хвилі відповідної довжини, які йдуть з мінімальною швидкістю, а попереду них з більшою швидкістю побіжать короткі і дуже довгі хвилі. У будь-якій водоймі можна легко побачити дуже короткі хвилі, а от довгі хвилі спостерігати важче.

Таким чином, ми переконалися, що брижі, яка настільки часто використовується для ілюстрації простих хвиль, насправді набагато складніше і цікавіше: у неї немає різкого хвильового фронту, як у випадку простих хвиль, подібних звуку або світла. Основна хвиля, яка виривається вперед, складається з дрібних брижах. Завдяки дисперсії різке обурення поверхні води не призводить до різкої хвилі. Першими все одно йдуть дуже дрібні хвилі. У всякому разі, коли по воді з деякою швидкістю рухається об'єкт, то виникає дуже складна картина, оскільки різні хвилі йдуть з різною швидкістю. Взявши корито з водою, можна легко продемонструвати, що найшвидшими будуть дрібні капілярні хвилі, а вже за ними йдуть більші. Крім того, нахиливши корито, можна побачити, що там, де менше глибина, менше і швидкість. Якщо хвиля йде під якимось кутом до лінії максимального нахилу, то вона загортає в сторону цієї лінії. Таким способом можна продемонструвати безліч різних речей і прийти до висновку, що хвилі на воді - куди більш складна річ, ніж хвилі в повітрі.

Швидкість довгих хвиль з круговим рухом води зменшується на дрібному місці і збільшується на глибокому. Таким чином, коли хвиля йде до берега, де глибина менше, вона сповільнюється. Але там, де вода глибше, хвиля рухається швидше, так що ми знову стикаємося з механізмом ударної хвилі. Однак на цей раз, оскільки хвиля не настільки проста, ударний фронт її набагато більше спотворений: хвиля «перегинається через себе» самим звичним для нас чином (фіг. 51.12). Саме це ми бачимо, коли хвиля набігає на берег: у ній виявляються всі притаманні природі труднощі. Нікому досі не вдалося обчислити форму хвилі в той момент, коли вона розбивається. Це дуже легко зробити, коли хвилі малі, але коли вони стають великими, все занадто ускладнюється.

Цікава властивість капілярних хвиль можна спостерігати при обуренні поверхні, що рухається. З точки зору самого об'єкта вода тече повз нього, і хвилі, які в кінцевому підсумку залишаться разом з ним, завжди будуть хвилями, які як раз мають потрібну швидкість, щоб залишатися на воді разом з об'єктом. Точно так же якщо помістити об'єкт в потік, який буде омивати його, то картина хвиль виявиться стаціонарної і як раз потрібної довжини хвилі для того, щоб рухатися з тією ж швидкістю, що і вода. Але якщо групова швидкість менше фазової, то обурення йде по потоку назад, оскільки групова швидкість недостатня для того, щоб наздогнати потік. Якщо ж групова швидкість більше фазової, то хвильова картина з'явиться перед об'єктом. Якщо пильно стежити за пливли в потоці об'єктом, то можна помітити попереду нього невелику брижі, а позаду нього - довгі хвилі.

Інші цікаві явища подібного роду можна спостерігати в ллється рідини. Якщо, наприклад, швидко виливати молоко з пляшки, то можна помітити, як струмінь молока перетинається безліччю перехресних ліній. Це хвилі, викликані обуренням на краях пляшки; вони дуже схожі на хвилі, викликані об'єктом, пливли по потоку. Але тепер такий ефект виникає з обох сторін, тому виходить картина пересічних ліній.

Отже, ми познайомилися з деякими цікавими властивостями хвиль, з різними ускладненнями, залежними від фазової швидкості і довжини хвилі, а також із залежністю швидкості хвилі від глибини і т. Д .; все це призводить до вельми складним, а тому і цікавих явищ природи.